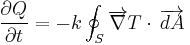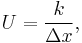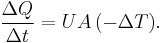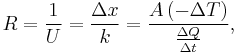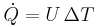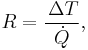Conduction (heat)
In heat transfer, conduction (or heat conduction) is the transfer of thermal energy between neighboring molecules in a substance due to a temperature gradient. It always takes place from a region of higher temperature to a region of lower temperature, and acts to equalize the temperature differences. Conduction takes place in all forms of matter, viz. solids, liquids, gases and plasmas, but does not require any bulk motion of matter. In solids, it is due to the combination of vibrations of the molecules in a lattice and the energy transport by free electrons. In gases and liquids, conduction is due to the collisions and diffusion of the molecules during their random motion.
Heat can also be transferred by radiation and/or convection, and often more than one of these processes occurs in a given situation.
Contents |
Overview
On a microscopic scale, conduction occurs as hot, rapidly moving or vibrating atoms and molecules interact with neighboring atoms and molecules, transferring some of their energy (heat) to these neighboring atoms. In other words, heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in contact. Conduction is greater in solids because the network of relatively fixed spacial relationships between atoms helps to transfer energy between them by vibration.
As density decreases so does conduction. Therefore, fluids (and especially gases) are less conductive. This is due to the large distance between atoms in a gas: fewer collisions between atoms means less conduction. Conductivity of gases increases with temperature. Conductivity increases with increasing pressure from vacuum up to a critical point that the density of the gas is such that molecules of the gas may be expected to collide with each other before they transfer heat from one surface to another. After this point conductivity increases only slightly with increasing pressure and density.
The inter-molecular transfer of energy could be primarily by elastic impact as in fluids or by free electron diffusion as in metals or phonon vibration as in insulators. In insulators the heat flux is carried almost entirely by phonon vibrations.
Metals (e.g. copper, platinum, gold,etc.) are usually the best conductors of thermal energy. This is due to the way that metals are chemically bonded: metallic bonds (as opposed to covalent or ionic bonds) have free-moving electrons which are able to transfer thermal energy rapidly through the metal. The "electron fluid" of a conductive metallic solid conducts nearly all of the heat flux through the solid. Phonon flux is still present, but carries less than 1% of the energy. Electrons also conduct electric currentthrough conductive solids, and the thermal and electrical conductivities of most metals have about the same ratio. A good electrical conductor, such as copper, usually also conducts heat well. The Peltier-Seebeck effect exhibits the propensity of electrons to conduct heat through an electrically conductive solid. Thermoelectricity is caused by the relationship between electrons, heat fluxes and electrical currents. Heat conduction within a solid is directly analogous to diffusion of particles within a fluid, in the situation where there are no fluid currents.
To quantify the ease with which a particular medium conducts, engineers employ the thermal conductivity, also known as the conductivity constant or conduction coefficient, k. In thermal conductivity k is defined as "the quantity of heat, Q, transmitted in time (t) through a thickness (L), in a direction normal to a surface of area (A), due to a temperature difference (ΔT) [...]." Thermal conductivity is a material property that is primarily dependent on the medium's phase, temperature, density, and molecular bonding.
Steady-state conduction
Steady state conduction is the form of conduction which happens when the temperature difference driving the conduction is constant so that after an equilibration time, the spatial distribution of temperatures (temperature field) in the conducting object does not change any further. For example, a bar may be cold at one end and hot at the other, but the gradient of temperatures along the bar do not change with time. The temperature at any given section of the rod remains constant, and this temperature varies linearly along the direction of heat transfer.
In steady state conduction, the amount of heat entering a section is equal to amount of heat coming out. In steady state conduction, all the laws of direct current electrical conduction can be applied to "heat currents". In such cases, it is possible to take "thermal resistances" as the analog to electrical resistances. Temperature plays the role of voltage and heat transferred is the analog of electrical current.
Transient conduction
There also exists non-steady-state situations, in which the temperature drop or increase occurs more drastically, such as when a hot copper ball is dropped into oil at a low temperature. Here the temperature field within the object changes as a function of time, and the interest lies in analysing this spatial change of temperature within the object over time. This mode of heat conduction can be referred to as transient conduction. Analysis of these systems is more complex and (except for simple shapes) calls for the application of approximation theories, and/or numerical analysis by computer. One popular graphical method involves the use of Heisler Charts.
Relativistic conduction
The theory of relativistic heat conduction is a model that is compatible with the theory of special relativity. For most of the last century, it was recognized that Fourier equation is in contradiction with the theory of relativity because it admits an infinite speed of propagation of heat signals. For example, according to Fourier equation, a pulse of heat at the origin would be felt at infinity instantaneously. The speed of information propagation is faster than the speed of light in vacuum, which is physically inadmissible within the framework of relativity. Alterations to the Fourier model provided for a relativistic model of heat conduction, avoiding this problem.
Fourier's law
The law of Heat Conduction, also known as Fourier's law, states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat is flowing. We can state this law in two equivalent forms: the integral form, in which we look at the amount of energy flowing into or out of a body as a whole, and the differential form, in which we look at the flows or fluxes of energy locally.
Differential form
The differential form of Fourier's Law of thermal conduction shows that the local heat flux, 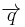 , is equal to the product of thermal conductivity,
, is equal to the product of thermal conductivity, 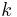 , and the negative local temperature gradient,
, and the negative local temperature gradient, 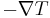 . The heat flux is the amount of energy that flows through a particular surface per unit area per unit time.
. The heat flux is the amount of energy that flows through a particular surface per unit area per unit time.
where (including the SI units)
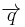 is the local heat flux, W·m−2
is the local heat flux, W·m−2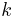 is the material's conductivity, W·m−1·K−1,
is the material's conductivity, W·m−1·K−1,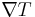 is the temperature gradient, K·m−1.
is the temperature gradient, K·m−1.
The thermal conductivity, 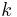 , is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case
, is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case 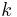 is represented by a second-order tensor. In nonuniform materials,
is represented by a second-order tensor. In nonuniform materials, 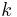 varies with spatial location.
varies with spatial location.
For many simple applications, Fourier's law is used in its one-dimensional form. In the x-direction,
Integral form
By integrating the differential form over the material's total surface  , we arrive at the integral form of Fourier's law:
, we arrive at the integral form of Fourier's law:
where (including the SI units)
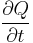 is the amount of heat transferred per unit time (in W) and
is the amount of heat transferred per unit time (in W) and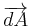 is an oriented surface area element (in m2)
is an oriented surface area element (in m2)
The above differential equation, when integrated for a homogeneous material of 1-D geometry between two endpoints at constant temperature, gives the heat flow rate as:
where
- A is the cross-sectional surface area,
 is the temperature difference between the ends,
is the temperature difference between the ends,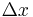 is the distance between the ends.
is the distance between the ends.
This law forms the basis for the derivation of the heat equation. Ohm's law is the electrical analogue of Fourier's law.
Conductance
Writing
where U is the conductance, in W/(m2 K).
Fourier's law can also be stated as:
The reciprocal of conductance is resistance, R, given by:
and it is resistance which is additive when several conducting layers lie between the hot and cool regions, because A and Q are the same for all layers. In a multilayer partition, the total conductance is related to the conductance of its layers by:
So, when dealing with a multilayer partition, the following formula is usually used:
When heat is being conducted from one fluid to another through a barrier, it is sometimes important to consider the conductance of the thin film of fluid which remains stationary next to the barrier. This thin film of fluid is difficult to quantify, its characteristics depending upon complex conditions of turbulence and viscosity, but when dealing with thin high-conductance barriers it can sometimes be quite significant.
Intensive-property representation
The previous conductance equations, written in terms of extensive properties, can be reformulated in terms of intensive properties.
Ideally, the formulae for conductance should produce a quantity with dimensions independent of distance, like Ohm's Law for electrical resistance: 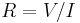 , and conductance:
, and conductance:  .
.
From the electrical formula:  , where ρ is resistivity, x = length, and A is cross-sectional area, we have
, where ρ is resistivity, x = length, and A is cross-sectional area, we have 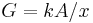 , where G is conductance, k is conductivity, x = length, and A = cross-sectional area.
, where G is conductance, k is conductivity, x = length, and A = cross-sectional area.
For Heat,
where U is the conductance.
Fourier's law can also be stated as:
analogous to Ohm's law: 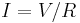 or
or 
The reciprocal of conductance is resistance, R, given by:
analogous to Ohm's law: 
The rules for combining resistances and conductances (in series and in parallel) are the same for both heat flow and electric current.
Cylinders
Conduction through cylinders can be calculated when variables such as the internal radius 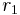 , the external radius
, the external radius 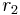 , and the length denoted as
, and the length denoted as 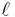 .
.
The temperature difference between the inner and outer wall can be expressed as 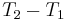 .
.
The area of the heat flow: 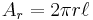
When Fourier’s equation is applied:
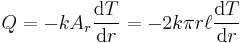
Rearranged:
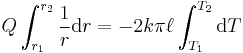
Therefore the rate of heat transfer is

The thermal resistance is
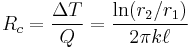
And 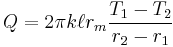 , where
, where 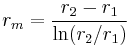 and it is important to note that this is the log-mean radius.
and it is important to note that this is the log-mean radius.
See also
- Heat
- Thermal conductivity
- Heat flux
- Heat transfer
- Convection
- Convection diffusion equation
- Thermal radiation
- Thermal contact conductance
- U-value (insulation)
- Heat pipe
- Fick's law of diffusion
- Relativistic heat conduction
- Churchill-Bernstein Equation
References
- Dehghani, F 2007, CHNG2801 – Conservation and Transport Processes: Course Notes, University of Sydney, Sydney
- John H Lienhard IV and John H Lienhard V, 'A Heat Transfer Textbook', Third Edition, Phlogyston Press, Cambridge Massachusetts [1]
External links
- Newton's Law of Cooling by Jeff Bryant based on a program by Stephen Wolfram, Wolfram Demonstrations Project.
- When Will My Turkey Be Done? is an example of applied heat conduction equations similar to Newton's Law of Cooling which predict the cooking time of turkeys and other roasts.